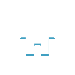?u?x=1，?u?y=-1，?u?z=0

    3.求u=ln(sin(xy))的全微分

    1秒，只用了1秒，李默直接写下了答案。

    du=(?u?x)dx+(?u?y)dy?u?x=y[cos(xy)][sin(xy)]?u?y=x[cos(xy)][sin(xy)]du=(ydx+xdy)[cos(xy)][sin(xy)]

    ..........................

    .........................

    仅仅用时30分钟，李默就做完了《数学分析》的试卷，如果不是最后那道开放性题目，他用了6中方法阐述，还可以更快一点。

    下一张试卷是《高等代数》。

    1.设V1与V2分别是齐次方程组x1+x2+.....+xn=0及x1=x2=.....=xn的解空间，求V1，V2并证P^n=V1+V2，其中P^n为数域p上的n维向量空间。

    答案：V1就是向量bai(1，1，...，1)的正交补空间，基为(1，-1，0，0，...，0)，（du1，0，－zhi1，0，。。。，0），。。。，（1，0，。。。，－1），每个向量第dao一个分量为1，第k+1个分量为－1，其余分量为0，k＝1，2，。。。，n－1。V2的基为(1，1，1，...，1)。容易看出，V1和V2是正交的（基向量之间是正交的)，V1的维数是n－1，V2的维数是1，两者之和为n，因此两个子空间的和是直和，恰好是全空间。

    1分钟，就完成了第一题。自从灵智升到了2级，他觉得自己可以很轻松的抓住解题思路。

    旁边的周明看到李默已经完成了《数学分析》试卷，不由走到他身后，看了起来。只见眼前的稚嫩少年，做起题目像写文章一样，粉笔极速。

    即使遇到狡计的题目，少年眉头微颦，稍加思索，就可以迎刃而解。

    吴教授经常在自己面前夸耀数学系出了一位天才，本来周明还不相信。可以进入燕大数学系学习的哪个不是天才。

    可现在看到眼前这个飞速做题的少年，周明才真正明白天才的意思。

    《高等代数》试卷也很快的被李默完成了，周明下意识的看了一下自己的手机，只用了20分钟。

    下一张试卷就是《微积分方程》，《微积分方程》是以计算量大著称的。不是那种有了解题思路就可以轻松解决的题目。

    “这次看你需要多久？”周明这次特意看了一下自己的手机，现在是9点30分。

    第一道题目，设a，b，c都是正常数，且y(x)是微分方程ay''+by'+cy=0的一个解，求证：

    lim(n~+∞)y(x)=0。

    李默快速的在心中计算了一遍，写道：

    ar^2+br+c=0

    因为a，b，c0

    两根为r1，r2

    由伟达定理

    r1+r2=-ba0

    r1*r2=ca0

    若r1，r2为实根，则bai显然只有r1，r20可以满足du和小于零zhi，积大于零

    .......

    当x-正无穷时，exp(r1*x)，exp(r2*x)-0，所以y-0

    若是复根，则必为共轭复根，因为系数是实数

    所以r1=m+in，r2=m-in

    r1+r2=2m=-ba0

    .......

    因为m

『加入书签，方便阅读』